pattern recognition
: classifying based on the features
http://en.wikipedia.org/wiki/Pattern_recognition
Knowledge about objects and their classes gives the necessary information for object classification.
381p
artificial intelligence (AI)
http://en.wikipedia.org/wiki/Artificial_intelligence
http://en.wikipedia.org/wiki/Knowledge_representation
- simple control strategies
- a rich, well structured representation of a large set of a priori data and hypotheses
syntax
-> the symbols that may be used and the ways that they may be arranged
semantics
-> how meaning is embodied in the symbols and the symbol arrangement allowed by the syntax
representation
-> a set of syntactic and semantic conventions that make it possible ot describe things
formal grammars and languages
predicate logic
production rules
semantic nets
frames
-> data structures (lists, trees, graphs, tables, hierarchies, sets, rings, nets, and matrices)
Descriptions, features
: scalar properties of objects -> feature vectors
Grammars, languages
- structures from primitives (elementary structural properties of the objects) and the relations between them
-> rules defining how the chains, trees, or graphs can be constructed from a set of symbols (primitives)
Predicate logic (술어논리)
- combinations of logic variables (true/false), quantifiers, and logic operators
- modus ponens and resolution
- PROLOG
- 'pure truth'
-> logic conditions and constraints into knowledge processing
Production rules
- condition action pairs
- procedural character of knowledge
=> handling uncertainty information -> expert systems
Fuzzy logic
- some reasonable threshold
- fuzzy rule
- linguistic variables
Semantic nets
- objects, their description, and a description of relations between objects
- local information and local knowledge
- relations between partial representations described at all appropriate hierarchical levels (nodes: objects / arcs: relations between objects)
- degrees of closeness
Frames, scripts
- a substitute for missing information
-> to overcome the lack of continuous information
- a tool for organizing knowledge in prototypical objects, and for description of mutual influences of objects using stereotypes of behavior in specific situations
386p
pattern
: formal description of sensed objects
The classes form clusters in the feature space, which can be separated by a discrimination curve (or hyper-surface in a multi-dimensional feature space).
If the discrimination hyper-surfaces are hyper-planes, it is called a linearly separable task.
387p
9.2.1 Classification principles
output - decision about the class of the object
class identifiers - generated output symbols
decision rule - the function describing relations between the classifier inputs and the output
discrimination functions - scalar functions defining the discrimination hyper-surfaces
The determination of discrimination hyper-surfaces (or definition of the decision rule) is the goal of classifier design.
decision rule of a classifier
(1) find a maximum discrimination function -> linear classifier
(2) calculate the minimum distance from exemplars (sample patterns) -> piecewise linear discrimination hyper-planes
Φ-classifier
non-linear discrimination hypersurfaces of the original feature space -- non-linear transformation --> hyper-planes in the transformed freature space
390p
9.2.2 Classifier setting
Settings of the optimal classifier should be probabilistic.
optimality criteria: the value of the mean loss caused by classification
optimum decision rule:
minimum mean loss + the vector of optimal parameters
(1) minimum error criterion (Bayes criterion, maximum likelihood)
minimum-loss optimality criterion
Bayes formula
- a posteriori probabilities of classes, the conditional probability densities of objects, a priori probability, the mixture density
theoretical optimum
: "no other classifier setting can give a lower probability of the decision loss."
(2) best approximation criterion
: the best approximation of discrimination functions by linear combinations of pre-determined functions
The information obtained from the elements of the training set must be generalized to cover the whole feature space.
(=> The classifier should be able to recognize even those objects that it has never seen before.)
sequential increase in training set size -> sequential processing of information -> classification correctness
learning: the process of automated system optimization based on the sequential presentation of examples, to minimize the optimality criterion
object description
- permissible classification error
- complexity of the classifier construction
- time required for classification
-> determination of informativity and discriminativity of measured features
393p
9.2.3 Classifier learning
(1) probability density estimation
-> minimum error criterion -> discriminant functions
priori information -> the shape of probability density functions => parametric learning
eg. normal distribution - dispersion matrix, mean value vector
+ priori estimate + confidence (weight)
(2) direct loss minimization
-> best approximation criterion -> decision rule
no prior information -> stochastic approximations
http://en.wikipedia.org/wiki/Stochastic_approximation
Jack Sklansky
Pattern Classifiers and Trainable Machines
minimum distance classifier
396p
9.2.4 Support Vector Machines
http://en.wikipedia.org/wiki/Support_vector_machines
maximizing the width of the empty area (margin) between the two classes
-> An optimal hypersurface has the lowest capacity.
The support vectors specify the discrimination function.
To maximize the margin, we need to minimize ∥w∥ for a quadratic programming optimization problem.
If we want to solve:
- maximize

- subject to

- subject to
We introduce a new variable (λ) called a Lagrange multiplier to rewrite the problem as:
- maximize

Solving this new unconstrained problem for x, y, and λ will give us the solution (x, y) for our original constrained problem. The gradients of f and g are parallel vectors at the maximum, since the gradients are always normal to the contour lines. This occurs just when the gradient of f has no component tangential to the level sets of g. This condition is equivalent to  for some λ.
for some λ.
and solve
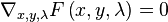 .
.
Lagrange duality
Given a convex optimization problem in standard form
with the domain  having non-empty interior, the Lagrangian function
having non-empty interior, the Lagrangian function  is defined as
is defined as
The vectors λ and ν are called the dual variables or Lagrange multiplier vectors associated with the problem. The Lagrange dual function  is defined as
is defined as
The dual function g is concave, even when the initial problem is not convex. The dual function yields lower bounds on the optimal value p * of the initial problem; for any  and any ν we have
and any ν we have 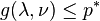 . If a constraint qualification such as Slater's condition holds and the original problem is convex, then we have strong duality, i.e.
. If a constraint qualification such as Slater's condition holds and the original problem is convex, then we have strong duality, i.e. 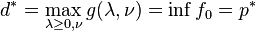 .
.
ref.
Lagrange Multipliers without Permanent Scarring Dan Klein (Assistant Professor, Computer Science Division, University of California at Berkeley)
http://en.wikipedia.org/wiki/Karush-Kuhn-Tucker_conditions
a generalization of the method of Lagrange multipliers to inequality constraints.
Each of the Lagrange multipliers shares the corresponding support vectors.
The discrimination hyperplane in the feature space can be obrained from vectors in the input space and dot products in the feature space.
ref.
Dmitriy Fradkin and Ilya Muchnik "Support Vector Machines for Classification" in J. Abello and G. Carmode (Eds) "Discrete Methods in Epidemiology", DIMACS Series in Discrete Mathematics and Theoretical Computer Science, volume 70, pp. 13-20, 2006.
Succinctly describes theoretical ideas behind SVM.
soft margin -> support vector machine
kernel trick to determine the similarity of two patterns
http://en.wikipedia.org/wiki/Kernel_trick
(eg. Gaussian radial basis fn. kernel -> Hilbert space)
402p
9.2.5 Cluster analysis
http://en.wikipedia.org/wiki/Cluster_analysis
1) MacQueen k-means
http://en.wikipedia.org/wiki/K-means_algorithm
within-cluster variance
2) ISODATA cluster analysis
3) mean shift algorithm
4) fuzzy c-means algorithm
5) expectation-maximazation algorithm
http://en.wikipedia.org/wiki/Expectation-maximization_algorithm
EM alternates between performing an expectation (E) step, which computes an expectation of the likelihood by including the latent variables as if they were observed, and a maximization (M) step, which computes the maximum likelihood estimates of the parameters by maximizing the expected likelihood found on the E step. The parameters found on the M step are then used to begin another E step, and the process is repeated.
404p
ref.
Ben Krose & Patrick van der Smagt <An introduction to Neural Networks>
9.3.1 Feed-forward networks
9.3.2 Unsupervised learning
9.3.3 Hopfield neural nets
http://en.wikipedia.org/wiki/Hopfield_neural_network
410p
9.4.1 Grammers and languages
formal language
9.4.2 Syntactic analysis, syntactic classifier
9.4.3 Syntactic classifier learning, grammar inference
418p
9.5.1 Isomorphism of graphs and sub-graphs
9.5.2 Similarity of graphs
424p
9.6.1 Genetic algorithms
Reproduction
Crossover
Mutation
9.6.2 Simulated annealing
430p
9.7.1 Fuzzy sets and fuzzy membership functions
'@GSMC > 박래홍: Computer Vision' 카테고리의 다른 글
| Ch.10 Image Understanding (0) | 2008.12.15 |
|---|---|
| 2.4 Color images & 2.5 Cameras (0) | 2008.10.16 |
| Ch. 6 Segmentation I (0) | 2008.09.20 |
| Ch. 2 The image, its representations and properties (0) | 2008.09.10 |
| Ch.1 Introduction (0) | 2008.09.04 |



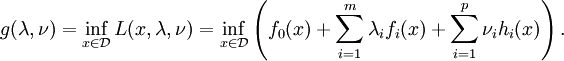
 lagrange-multipliers[1].pdf
lagrange-multipliers[1].pdf