보호되어 있는 글입니다.
내용을 보시려면 비밀번호를 입력하세요.
보호되어 있는 글입니다.
내용을 보시려면 비밀번호를 입력하세요.
| hw4 - non-linear least squares, illumination, least-squares model fitting (0) | 2008.12.08 |
|---|---|
| Lecture 10: Uncalibrated Multi-view Geometry - Reconstruction (0) | 2008.12.04 |
| Lecture 9: Multi-view Geometry (0) | 2008.12.04 |
| Lecture 8: Uncalibrated Multiple-View Geometry: Fundamental Matrix (0) | 2008.10.28 |
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
Projective reconstruction
= Affine upgrade (H_p) + Euclidean upgrade (H_a)
=> Auto-calibration
Kruppa equations
Range Imaging
Range Sensor Calibration
| hw4 - non-linear least squares, illumination, least-squares model fitting (0) | 2008.12.08 |
|---|---|
| Lecture 11: Light & Reflection (0) | 2008.12.04 |
| Lecture 9: Multi-view Geometry (0) | 2008.12.04 |
| Lecture 8: Uncalibrated Multiple-View Geometry: Fundamental Matrix (0) | 2008.10.28 |
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
| Lecture 11: Light & Reflection (0) | 2008.12.04 |
|---|---|
| Lecture 10: Uncalibrated Multi-view Geometry - Reconstruction (0) | 2008.12.04 |
| Lecture 8: Uncalibrated Multiple-View Geometry: Fundamental Matrix (0) | 2008.10.28 |
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
Fundamental Matrix
http://en.wikipedia.org/wiki/Fundamental_matrix_(computer_vision)
In computer vision, the fundamental matrix 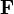 is a
is a  matrix of rank 2 which relates corresponding points in stereo images. In epipolar geometry, with homogeneous image coordinates
matrix of rank 2 which relates corresponding points in stereo images. In epipolar geometry, with homogeneous image coordinates  and
and  of corresponding points in a stereo image pair,
of corresponding points in a stereo image pair,  describes a line (an epipolar line) on which the corresponding point y2 on the other image must lie. That means, for all pairs of corresponding points holds
describes a line (an epipolar line) on which the corresponding point y2 on the other image must lie. That means, for all pairs of corresponding points holds

Being of rank two and determined only up to scale, the fundamental matrix can be estimated given at least seven point correspondences. Its seven parameters represent the only geometric information about cameras that can be obtained through point correspondences alone.
epipole
epipolar line
epipolar plane
http://en.wikipedia.org/wiki/Epipolar_geometry
RANdom SAmple Consensus
http://en.wikipedia.org/wiki/RANSAC
ref.
http://www.robots.ox.ac.uk/~vgg/hzbook/index.html
http://nonsense.danielwedge.com/2008/10/19/the-fundamental-matrix-song/
An Invitation to 3-D Vision
Yi Ma, Stefano Soatto, Jana Kosecka, Shankar Sastry
Springer Verlag, 2003
Learning Epipolar Geometry
The Java code for this page was created by Sylvain Bougnoux.
| Lecture 10: Uncalibrated Multi-view Geometry - Reconstruction (0) | 2008.12.04 |
|---|---|
| Lecture 9: Multi-view Geometry (0) | 2008.12.04 |
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
| Lecture 5: Single Camera View Geometry (0) | 2008.10.27 |
image filtering
image warping
LSI (Linear Shift Invariance) - convolution
http://en.wikipedia.org/wiki/Convolution
Convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions.
http://en.wikipedia.org/wiki/Cross_correlation
http://en.wikipedia.org/wiki/Gaussian_filter
Mathematically, a Gaussian filter modifies the input signal by convolution with a Gaussian function; this transformation is also known as the Weierstrass transform.
Gaussian filters are designed to give no overshoot to a step function input while minimizing the rise and fall time (which leads to the steepest possible slope). This behavior is closely connected to the fact that the Gaussian filter has the minimum possible group delay.
| Lecture 9: Multi-view Geometry (0) | 2008.12.04 |
|---|---|
| Lecture 8: Uncalibrated Multiple-View Geometry: Fundamental Matrix (0) | 2008.10.28 |
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
| Lecture 5: Single Camera View Geometry (0) | 2008.10.27 |
| Lecture 4: Projective Geometry (0) | 2008.10.26 |
Structure from Stereo
two or more images, calibrated cameras (K(f), R, T known)
http://en.wikipedia.org/wiki/Stereo_vision
ref.
UCR stereographs
http://www.cmp.ucr.edu/site/exhibitions/stereo/
The Art of Stereo Photography
http://www.photostuff.co.uk/stereo.htm
History of Stereo Photography
http://www.rpi.edu/~ruiz/stereo_history/text/historystereog.html
Double Exposure
http://home.centurytel.net/s3dcor/index.html
Stereo Photography
http://www.shortcourses.com/book01/chapter09.htm
3D Photography links
http://www.studyweb.com/links/5243.html
National Stereoscopic Association
http://204.248.144.203/3dLibrary/welcome.html
Books on Stereo Photography
http://userwww.sfsu.edu/~hl/3d.biblio.html
http://en.wikipedia.org/wiki/Epipolar_geometry
http://en.wikipedia.org/wiki/Image_rectification
http://en.wikipedia.org/wiki/Rectification_(geometry)
Computing Rectifying Homographies for Stereo Vision
Charles Loop, Zhengyou Zhang
SSD (Sum of Squared Difference) to choose the baseline
Structure from Motion
http://en.wikipedia.org/wiki/Structure_from_motion
http://en.wikipedia.org/wiki/Motion_field
http://en.wikipedia.org/wiki/Nodal_point#Nodal_points
optical flow, image flow
http://en.wikipedia.org/wiki/Optical_flow
Horn-Schunck Algorithm
http://en.wikipedia.org/wiki/Horn-Schunck_algorithm
Determining Optical Flow
| Lecture 8: Uncalibrated Multiple-View Geometry: Fundamental Matrix (0) | 2008.10.28 |
|---|---|
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
| Lecture 5: Single Camera View Geometry (0) | 2008.10.27 |
| Lecture 4: Projective Geometry (0) | 2008.10.26 |
| Lecture 3: Linear Algebra for Computer Vision (0) | 2008.10.26 |
Single View Metrology
http://en.wikipedia.org/wiki/VRML
VRML (Virtual Reality Modeling Language, pronounced vermal or by its initials, originally — before 1995 — known as the Virtual Reality Markup Language) is a standard file format for representing 3-dimensional (3D) interactive vector graphics, designed particularly with the World Wide Web in mind. It has been superseded by X3D.
3-D Metrology
http://research.microsoft.com/~antcrim/
single view reconstruction
http://en.wikipedia.org/wiki/Ground_truth
radial distortion
http://en.wikipedia.org/wiki/Distortion_(optics)
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
|---|---|
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
| Lecture 4: Projective Geometry (0) | 2008.10.26 |
| Lecture 3: Linear Algebra for Computer Vision (0) | 2008.10.26 |
| Lecture 2: Image Formation & Camera Calibration (0) | 2008.10.24 |
A point in the image is a ray in projective space.
=> All points on the ray are equivalent.
http://en.wikipedia.org/wiki/Grassman_algebra
vanishing point
http://mathdl.maa.org/mathDL/1//?pa=content&sa=viewDocument&nodeId=477&bodyId=598
vanishing line
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
|---|---|
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
| Lecture 5: Single Camera View Geometry (0) | 2008.10.27 |
| Lecture 3: Linear Algebra for Computer Vision (0) | 2008.10.26 |
| Lecture 2: Image Formation & Camera Calibration (0) | 2008.10.24 |
eigen value
eigen vector
matrix rank
symmetric matrix
http://en.wikipedia.org/wiki/Symmetric_matrix
eigenvalue decomposition
http://en.wikipedia.org/wiki/Spectral_theorem
singular value decomposition
http://en.wikipedia.org/wiki/Singular_value_decomposition
linear equations
- inhomogeneous equations
- homogeneous equations - unconstrained / constrained
triangular decompostion:
QR, LL, LU decomposition
QR decomposition
http://en.wikipedia.org/wiki/QR_decomposition
- householder transformation
http://en.wikipedia.org/wiki/Householder_transformation
- Givens rotation
http://en.wikipedia.org/wiki/Givens_rotation
- Gram-Schmidt transformation
http://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process
Cholesky LL decomposition
http://en.wikipedia.org/wiki/Cholesky_decomposition
LU decomposition
ref. http://rkb.home.cern.ch/rkb/AN16pp/node160.html#SECTION0001600000000000000000
http://en.wikipedia.org/wiki/LU_decomposition
nonlinear optimization
http://en.wikipedia.org/wiki/Newton%27s_method
http://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
http://en.wikipedia.org/wiki/Linear_least_squares
cf. nonlinear least squares
http://en.wikipedia.org/wiki/Non-linear_least_squares
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
|---|---|
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
| Lecture 5: Single Camera View Geometry (0) | 2008.10.27 |
| Lecture 4: Projective Geometry (0) | 2008.10.26 |
| Lecture 2: Image Formation & Camera Calibration (0) | 2008.10.24 |
http://en.wikipedia.org/wiki/Pinhole_camera
Cameras using small apertures, and the human eye in bright light both act like a pinhole camera. The smaller the hole, the sharper the image, but the dimmer the projected image. Optimally, the size of the aperture, should be 1/100 or less of the distance between it and the screen.
http://en.wikipedia.org/wiki/Projection_matrix
a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged. Though abstract, this definition of "projection" formalizes and generalizes the idea of graphical projection.
http://en.wikipedia.org/wiki/Orthographic_projection
Increasing the focal length and distance of the camera to infinity in a perspective projection results in an orthographic projection. It is a form of parallel projection, where the view direction is orthogonal to the projection plane.
http://en.wikipedia.org/wiki/Homogeneous_coordinate
The homogeneous coordinates of a point of projective space of dimension n are usually written as (x : y : z : ... : w), a row vector of length n + 1, other than (0 : 0 : 0 : ... : 0). Two sets of coordinates that are proportional denote the same point of projective space: for any non-zero scalar c from the underlying field K, (cx : cy : cz : ... : cw) denotes the same point. Therefore this system of coordinates can be explained as follows: if the projective space is constructed from a vector space V of dimension n + 1, introduce coordinates in V by choosing a basis, and use these in P(V), the equivalence classes of proportional non-zero vectors in V.
http://en.wikipedia.org/wiki/Affine_transformation
In geometry, an affine transformation or affine map or an affinity (from the Latin, affinis, "connected with") between two vector spaces (strictly speaking, two affine spaces) consists of a linear transformation followed by a translation:

In the finite-dimensional case each affine transformation is given by a matrix A and a vector b, satisfying certain properties described below.
Physically, an affine transformation is one that preserves
In general, an affine transform is composed of zero or more linear transformations (rotation, scaling or shear) and a translation (or "shift"). Several linear transformations can be combined into a single matrix, thus the general formula given above is still applicable.
http://en.wikipedia.org/wiki/Projective_space
The idea of a projective space relates to perspective, more precisely to the way an eye or a camera projects a 3D scene to a 2D image. All points which lie on a projection line (i.e. a "line-of-sight"), intersecting with the focal point of the camera, are projected onto a common image point. In this case the vector space is R3 with the camera focal point at the origin and the projective space corresponds to the image points.
( For example, in the standard geometry for the plane two lines always intersect at a point except when the lines are parallel. In a projective representation of lines and points, however, such an intersection point exists even for parallel lines, and it can be computed in the same way as other intersection points. )
http://en.wikipedia.org/wiki/Projective_geometry
Projective geometry is the most general and least restrictive in the hierarchy of fundamental geometries, i.e. Euclidean - metric (similarity) - affine - projective. It is an intrinsically non-metrical geometry, whose facts are independent of any metric structure. Under the projective transformations, the incidence structure and the cross-ratio are preserved. It is a non-Euclidean geometry. In particular, it formalizes one of the central principles of perspective art: that parallel lines meet at infinity and therefore are to be drawn that way. In essence, a projective geometry may be thought of as an extension of Euclidean geometry in which the "direction" of each line is subsumed within the line as an extra "point", and in which a "horizon" of directions corresponding to coplanar lines is regarded as a "line". Thus, two parallel lines will meet on a horizon line in virtue of their possessing the same direction.
http://en.wikipedia.org/wiki/Camera_resectioning
When a camera is used, light from the environment is focused on an image plane and captured. This process reduces the dimensions of the data taken in by the camera from three to two (light from a 3D scene is stored on a 2D image). Each pixel on the image plane therefore corresponds to a shaft of light from the original scene. Camera resectioning determines which incoming light is associated with each pixel on the resulting image.
http://en.wikipedia.org/wiki/Camera_matrix
Since the camera matrix is involved in the mapping between elements of two projective spaces, it too can be regarded as a projective element. This means that it has only 11 degrees of freedom since any multiplication by a non-zero scalar results in an equivalent camera matrix.
http://en.wikipedia.org/wiki/Euclidean_space
An n-dimensional space with notions of distance and angle that obey the Euclidean relationships is called an n-dimensional Euclidean space.
An essential property of a Euclidean space is its flatness. Other spaces exist in geometry that are not Euclidean.
http://en.wikipedia.org/wiki/Euclidean_transformation
The Euclidean group E(n) is a subgroup of the affine group for n dimensions, and in such a way as to respect the semidirect product structure of both groups.
1. by a pair (A, b), with A an n×n orthogonal matrix, and b a real column vector of size n; or
2. by a single square matrix of size n + 1, as explained for the affine group.
http://en.wikipedia.org/wiki/Orthogonal_matrix

http://en.wikipedia.org/wiki/Singular_value_decomposition

where U is an m-by-m unitary matrix over K, the matrix Σ is m-by-n diagonal matrix with nonnegative numbers on the diagonal, and V* denotes the conjugate transpose of V, an n-by-n unitary matrix over K. Such a factorization is called a singular-value decomposition of M.
A common convention is to order the values Σi,i in non-increasing fashion. In this case, the diagonal matrix Σ is uniquely determined by M (though the matrices U and V are not).
http://en.wikipedia.org/wiki/Total_least_squares
total least squares = errors in variables = rigorous least squares = orthogonal regression
http://en.wikipedia.org/wiki/RQ_decomposition#Relation_to_RQ_decomposition
| Lecture 7: Image Filtering & Edge Detection (0) | 2008.10.28 |
|---|---|
| Lecture 6: Multiple-View Geometry: Stereo, Motion, Features (0) | 2008.10.27 |
| Lecture 5: Single Camera View Geometry (0) | 2008.10.27 |
| Lecture 4: Projective Geometry (0) | 2008.10.26 |
| Lecture 3: Linear Algebra for Computer Vision (0) | 2008.10.26 |