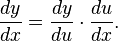2009. 1. 9. 11:03
@GSMC/서용덕: Convex Optimization
해석학 解析學
대수학과 기하학에 대하여, 함수의 연속성에 관한 성질을 미분 및 적분의 개념을 기초로 하여 연구하는 수학. 미적분학, 미분 방정식론, 적분 방정식론, 집합론, 실함수론, 복소수 함수론 따위가 있다
http://en.wikipedia.org/wiki/Mathematical_analysis
대수학 (代數學)
개개의 숫자 대신에 숫자를 대표하는 일반적인 문자를 사용하여 수의 관계, 성질, 계산 법칙 따위를 연구하는 학문. 현재는 덧셈이나 곱셈 같은 요소 간의 결합이 정의된 집합, 즉 대수계를 연구하는 학문도 포괄한다.
http://en.wikipedia.org/wiki/Algebra
the study of structure, relation, and quantity
Linear algebra, in which the specific properties of vector spaces are studied (including matrices);
선형대수학 (線型代數學)
벡터, 행렬, 행렬식, 벡터 공간, 선형 사상 따위를 연구하는 학문. 대수학의 한 분야이다.
A.1 Norms
A.1.1 Inner product, Euclidean norm, and angle
In mathematics, the dot product, also known as the scalar product, is an operation which takes two vectors over the real numbers R and returns a real-valued scalar quantity. It is the standard inner product of the orthonormal Euclidean space.
( Inner product spaces generalize Euclidean spaces (in which the inner product is the dot product, also known as the scalar product) to vector spaces of any (possibly infinite) dimension, and are studied in functional analysis. )
http://en.wikipedia.org/wiki/Norm_(mathematics)#Euclidean_norm
a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector.
The Euclidean norm is often known as the magnitude.
http://en.wikipedia.org/wiki/Lp_space
spaces of p-power integrable functions, and corresponding sequence spaces. They are sometimes called Lebesgue spaces
http://en.wikipedia.org/wiki/Cauchy-Schwarz_inequality
http://en.wikipedia.org/wiki/Frobenius_norm#Frobenius_norm
A.1.2 Norms, distance, and unit ball
http://en.wikipedia.org/wiki/Homogeneous_function
a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor.
(In mathematics, science (including computer science), linguistics and engineering, an argument is, generally speaking, an independent variable or input to a function.)
http://en.wikipedia.org/wiki/Triangle_inequality




http://en.wikipedia.org/wiki/Unit_sphere
a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point

http://en.wikipedia.org/wiki/Closure_(topology)
Let S be a subset of a topological space X. Then x is a point of closure of S if every neighbourhood of x contains a point of S.
A.2 Analysis
A.3 Functions
A.4 Derivatives
A.4.1 Derivative and gradient
http://en.wikipedia.org/wiki/Derivative
int dom = interior domain
http://en.wikipedia.org/wiki/Domain_(mathematics)
In general, the interior of something refers to the space or part inside of it, excluding any kind of wall or boundary around its outside.
In mathematics, the interior of a set S consists of all points of S that are intuitively "not on the edge of S". A point that is in the interior of S is an interior point of S.
http://planetmath.org/?op=getobj&from=objects&id=3123
http://en.wikipedia.org/wiki/Jacobian
Jacobian Matrix = the matrix of all first-order partial derivatives of a vector-valued function. That is, the Jacobian of a function describes the orientation of a tangent plane to the function at a given point.
http://en.wikipedia.org/wiki/Exterior_derivative
http://en.wikipedia.org/wiki/Open_set
a set U is called open if, intuitively speaking, starting from any point x in U one can move by a small amount in any direction and still be in the set U. In other words, the distance between any point x in U and the edge of U is always greater than zero. (The openness property of a set is not topologically intrinsic. Taking a half-interval as a stand-alone space then it is open, since by definition the whole space is both open and closed. Virtually, the term open is applied to subsets.)
http://en.wikipedia.org/wiki/Gradient
the gradient of a scalar field is a vector field which points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change.
A generalization of the gradient for functions on a Euclidean space which have values in another Euclidean space is the Jacobian. A further generalization for a function from one Banach space to another is the Fréchet derivative.
http://en.wikipedia.org/wiki/Symmetric_matrix
(Using the Jordan normal form, one can prove that every square real matrix can be written as a product of two real symmetric matrices, and every square complex matrix can be written as a product of two complex symmetric matrices. (Bosch, 1986))
http://en.wikipedia.org/wiki/Basis_(linear_algebra)
a basis is a set of vectors that, in a linear combination, can represent every vector in a given vector space or free module, and such that no element of the set can be represented as a linear combination of the others. In other words, a basis is a linearly independent spanning set.
http://en.wikipedia.org/wiki/Basis_(topology)
a base (or basis) B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T.
http://en.wikipedia.org/wiki/Affine_transformation
an affine transformation or affine map or an affinity (from the Latin, affinis, "connected with") between two vector spaces (strictly speaking, two affine spaces) consists of a linear transformation followed by a translation:
http://en.wikipedia.org/wiki/Transformation_(geometry)
a transformation could be any function from a set X to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself which preserves this structure.
http://en.wikipedia.org/wiki/Trace_(linear_algebra)
the trace of a matrix is the sum of its eigenvalues, making it an invariant with respect to a change of basis.
The trace of the identity matrix is the dimension of the space.
http://en.wikipedia.org/wiki/Jordan_normal_form
http://en.wikipedia.org/wiki/Eigenvalue,_eigenvector_and_eigenspace
A.4.2 Chain rule
http://en.wikipedia.org/wiki/Chain_rule
http://en.wikipedia.org/wiki/Directional_derivative
A.4.3 Second derivative
대수학과 기하학에 대하여, 함수의 연속성에 관한 성질을 미분 및 적분의 개념을 기초로 하여 연구하는 수학. 미적분학, 미분 방정식론, 적분 방정식론, 집합론, 실함수론, 복소수 함수론 따위가 있다
http://en.wikipedia.org/wiki/Mathematical_analysis
대수학 (代數學)
개개의 숫자 대신에 숫자를 대표하는 일반적인 문자를 사용하여 수의 관계, 성질, 계산 법칙 따위를 연구하는 학문. 현재는 덧셈이나 곱셈 같은 요소 간의 결합이 정의된 집합, 즉 대수계를 연구하는 학문도 포괄한다.
http://en.wikipedia.org/wiki/Algebra
the study of structure, relation, and quantity
Linear algebra, in which the specific properties of vector spaces are studied (including matrices);
선형대수학 (線型代數學)
벡터, 행렬, 행렬식, 벡터 공간, 선형 사상 따위를 연구하는 학문. 대수학의 한 분야이다.
A.1 Norms
A.1.1 Inner product, Euclidean norm, and angle
In mathematics, the dot product, also known as the scalar product, is an operation which takes two vectors over the real numbers R and returns a real-valued scalar quantity. It is the standard inner product of the orthonormal Euclidean space.
( Inner product spaces generalize Euclidean spaces (in which the inner product is the dot product, also known as the scalar product) to vector spaces of any (possibly infinite) dimension, and are studied in functional analysis. )
http://en.wikipedia.org/wiki/Norm_(mathematics)#Euclidean_norm
a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector.
The Euclidean norm is often known as the magnitude.
http://en.wikipedia.org/wiki/Lp_space
spaces of p-power integrable functions, and corresponding sequence spaces. They are sometimes called Lebesgue spaces
http://en.wikipedia.org/wiki/Cauchy-Schwarz_inequality
http://en.wikipedia.org/wiki/Frobenius_norm#Frobenius_norm
A.1.2 Norms, distance, and unit ball
http://en.wikipedia.org/wiki/Homogeneous_function
a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor.
(In mathematics, science (including computer science), linguistics and engineering, an argument is, generally speaking, an independent variable or input to a function.)
http://en.wikipedia.org/wiki/Triangle_inequality




http://en.wikipedia.org/wiki/Unit_sphere
a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point

http://en.wikipedia.org/wiki/Closure_(topology)
Let S be a subset of a topological space X. Then x is a point of closure of S if every neighbourhood of x contains a point of S.
A.2 Analysis
A.3 Functions
A.4 Derivatives
A.4.1 Derivative and gradient
http://en.wikipedia.org/wiki/Derivative
int dom = interior domain
http://en.wikipedia.org/wiki/Domain_(mathematics)
In general, the interior of something refers to the space or part inside of it, excluding any kind of wall or boundary around its outside.
In mathematics, the interior of a set S consists of all points of S that are intuitively "not on the edge of S". A point that is in the interior of S is an interior point of S.
http://planetmath.org/?op=getobj&from=objects&id=3123
http://en.wikipedia.org/wiki/Jacobian
Jacobian Matrix = the matrix of all first-order partial derivatives of a vector-valued function. That is, the Jacobian of a function describes the orientation of a tangent plane to the function at a given point.
http://en.wikipedia.org/wiki/Exterior_derivative
http://en.wikipedia.org/wiki/Open_set
a set U is called open if, intuitively speaking, starting from any point x in U one can move by a small amount in any direction and still be in the set U. In other words, the distance between any point x in U and the edge of U is always greater than zero. (The openness property of a set is not topologically intrinsic. Taking a half-interval as a stand-alone space then it is open, since by definition the whole space is both open and closed. Virtually, the term open is applied to subsets.)
http://en.wikipedia.org/wiki/Gradient
the gradient of a scalar field is a vector field which points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change.
A generalization of the gradient for functions on a Euclidean space which have values in another Euclidean space is the Jacobian. A further generalization for a function from one Banach space to another is the Fréchet derivative.
http://en.wikipedia.org/wiki/Symmetric_matrix
(Using the Jordan normal form, one can prove that every square real matrix can be written as a product of two real symmetric matrices, and every square complex matrix can be written as a product of two complex symmetric matrices. (Bosch, 1986))
http://en.wikipedia.org/wiki/Basis_(linear_algebra)
a basis is a set of vectors that, in a linear combination, can represent every vector in a given vector space or free module, and such that no element of the set can be represented as a linear combination of the others. In other words, a basis is a linearly independent spanning set.
http://en.wikipedia.org/wiki/Basis_(topology)
a base (or basis) B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T.
http://en.wikipedia.org/wiki/Affine_transformation
an affine transformation or affine map or an affinity (from the Latin, affinis, "connected with") between two vector spaces (strictly speaking, two affine spaces) consists of a linear transformation followed by a translation:
In the finite-dimensional case each affine transformation is given by a matrix A and a vector b, satisfying certain properties described below.
http://en.wikipedia.org/wiki/Transformation_(geometry)
a transformation could be any function from a set X to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself which preserves this structure.
http://en.wikipedia.org/wiki/Trace_(linear_algebra)
the trace of a matrix is the sum of its eigenvalues, making it an invariant with respect to a change of basis.
The trace of the identity matrix is the dimension of the space.
http://en.wikipedia.org/wiki/Jordan_normal_form
http://en.wikipedia.org/wiki/Eigenvalue,_eigenvector_and_eigenspace
A.4.2 Chain rule
http://en.wikipedia.org/wiki/Chain_rule
http://en.wikipedia.org/wiki/Directional_derivative
A.4.3 Second derivative
'@GSMC > 서용덕: Convex Optimization' 카테고리의 다른 글
| [Boyd & Vandenberghe] Chapter 2 Convex Sets (0) | 2009.02.23 |
|---|---|
| [Boyd & Vandenberghe] Chapter 1 Introduction (0) | 2009.02.19 |
| [Boyd & Vandenberghe] Appendix C: Numerical linear algebra background (0) | 2009.02.02 |
| [Boyd & Vandenberghe] Appendix B: Problems involving two quadratic functions (0) | 2009.01.22 |
| Boyd & Vandenberghe <Convex Optimization> (0) | 2009.01.05 |