2007. 7. 25. 23:10
Code/NodeBox
The mission:
노드박스에서는 (프로세싱과 달리) draw()가 실행될 때마다 자동으로 background를 깔아 주므로 애니메이션을 구현하기는 편리하나, 자취를 남기는 방법에 대해서는 따로 생각해 주어야 한다.
위 코드에서 파란색 라인을 넣지 않으면 아래와 같이 다음 선분이 그려지면서 원 안에 자국이 남는다.
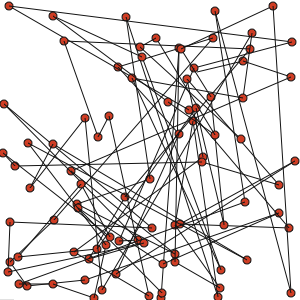
이를 없애기 위해 추측했던 바가 맞아 떨어짐을 다음과 같이 확인할 수 있었다.
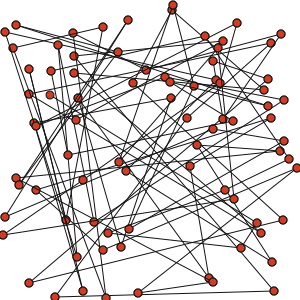
그런데 이 역시, 이후 랜덤하게 그려지는 선들이 기존의 꼭지점들과 교차하면서 나타나는 overlapping을 cover하지 못하고 있다. (이런 국적불명의 문장이란...) 고민해 봐야 할 문제다.
뭐, 이런 무식한 방법이 있기도 하다.
그리고 결과야 나온다. k가 증가할수록 속도가 느려져서 문제지.
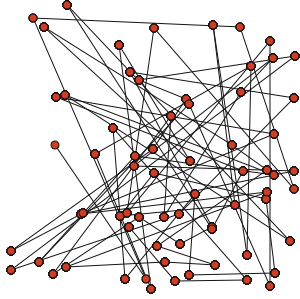
세상에... line과 oval이 관련되어 있다는 사실 때문에 p가 k에 dependent해야 하는 줄 알았었다. line과 oval은 종속변수를 공유하고 있을 뿐이며 오로지 그것으로 충분하다. simulation과 visualization의 차이를 다시 한 번 실감한다.
노드박스에서는 (프로세싱과 달리) draw()가 실행될 때마다 자동으로 background를 깔아 주므로 애니메이션을 구현하기는 편리하나, 자취를 남기는 방법에 대해서는 따로 생각해 주어야 한다.
s = 300
size(s, s)
speed(20)
def setup():
global x
global y
global f
f = 0
x = range(s)
y = range(s)
for i in range(s):
x[i] = random(s)
y[i] = random(s)
def draw():
global x
global y
global f
f += 1
if f >= s-1:
f = 0
for k in range(f):
stroke(0)
line(x[k], y[k], x[k+1], y[k+1])
fill(1, 0, 0)
ovalc(x[k+1], y[k+1], 8, 8)
ovalc(x[k], y[k], 8, 8) #to hide the segments of lines in ovals
def ovalc(cx, cy, w, h):
x = cx - w/2
y = cy - h/2
oval(x, y, w, h)
size(s, s)
speed(20)
def setup():
global x
global y
global f
f = 0
x = range(s)
y = range(s)
for i in range(s):
x[i] = random(s)
y[i] = random(s)
def draw():
global x
global y
global f
f += 1
if f >= s-1:
f = 0
for k in range(f):
stroke(0)
line(x[k], y[k], x[k+1], y[k+1])
fill(1, 0, 0)
ovalc(x[k+1], y[k+1], 8, 8)
ovalc(x[k], y[k], 8, 8) #to hide the segments of lines in ovals
def ovalc(cx, cy, w, h):
x = cx - w/2
y = cy - h/2
oval(x, y, w, h)
위 코드에서 파란색 라인을 넣지 않으면 아래와 같이 다음 선분이 그려지면서 원 안에 자국이 남는다.

이를 없애기 위해 추측했던 바가 맞아 떨어짐을 다음과 같이 확인할 수 있었다.

그런데 이 역시, 이후 랜덤하게 그려지는 선들이 기존의 꼭지점들과 교차하면서 나타나는 overlapping을 cover하지 못하고 있다. (이런 국적불명의 문장이란...) 고민해 봐야 할 문제다.
뭐, 이런 무식한 방법이 있기도 하다.
s = 300
d = 8
size(s, s)
speed(5)
def setup():
global x
global y
global f
f = 0
x = range(s)
y = range(s)
for i in range(s):
x[i] = random(d/2, s-d/2)
y[i] = random(d/2, s-d/2)
def draw():
global x
global y
global f
f += 1
if f >= s-1:
f = 0
for k in range(f):
stroke(0)
line(x[k], y[k], x[k+1], y[k+1])
for p in range(k+1):
fill(1, 0, 0)
ovalc(x[p+1], y[p+1], d, d)
ovalc(x[0], y[0], d, d)
def ovalc(cx, cy, w, h):
x = cx - w/2
y = cy - h/2
oval(x, y, w, h)
d = 8
size(s, s)
speed(5)
def setup():
global x
global y
global f
f = 0
x = range(s)
y = range(s)
for i in range(s):
x[i] = random(d/2, s-d/2)
y[i] = random(d/2, s-d/2)
def draw():
global x
global y
global f
f += 1
if f >= s-1:
f = 0
for k in range(f):
stroke(0)
line(x[k], y[k], x[k+1], y[k+1])
for p in range(k+1):
fill(1, 0, 0)
ovalc(x[p+1], y[p+1], d, d)
ovalc(x[0], y[0], d, d)
def ovalc(cx, cy, w, h):
x = cx - w/2
y = cy - h/2
oval(x, y, w, h)
그리고 결과야 나온다. k가 증가할수록 속도가 느려져서 문제지.

s = 300
d = 8
size(s, s)
speed(10)
def setup():
global x
global y
global f
global zz
f = 0
x = range(s)
y = range(s)
for i in range(s):
x[i] = random(d/2, s-d/2)
y[i] = random(d/2, s-d/2)
def draw():
global x
global y
global f
global zz
f += 1
if f >= s-1:
f = 0
for k in range(f):
stroke(0)
line(x[k], y[k], x[k+1], y[k+1])
for p in range(f):
fill(1, 0, 0)
ovalc(x[p+1], y[p+1], d, d)
ovalc(x[0], y[0], d, d)
def ovalc(cx, cy, w, h):
x = cx - w/2
y = cy - h/2
oval(x, y, w, h)
d = 8
size(s, s)
speed(10)
def setup():
global x
global y
global f
global zz
f = 0
x = range(s)
y = range(s)
for i in range(s):
x[i] = random(d/2, s-d/2)
y[i] = random(d/2, s-d/2)
def draw():
global x
global y
global f
global zz
f += 1
if f >= s-1:
f = 0
for k in range(f):
stroke(0)
line(x[k], y[k], x[k+1], y[k+1])
for p in range(f):
fill(1, 0, 0)
ovalc(x[p+1], y[p+1], d, d)
ovalc(x[0], y[0], d, d)
def ovalc(cx, cy, w, h):
x = cx - w/2
y = cy - h/2
oval(x, y, w, h)
세상에... line과 oval이 관련되어 있다는 사실 때문에 p가 k에 dependent해야 하는 줄 알았었다. line과 oval은 종속변수를 공유하고 있을 뿐이며 오로지 그것으로 충분하다. simulation과 visualization의 차이를 다시 한 번 실감한다.
'Code > NodeBox' 카테고리의 다른 글
| David Hirmes - lines15 (0) | 2007.08.01 |
|---|---|
| David Hirmes - lines14 (0) | 2007.07.31 |
| David Hirmes - blobs01 (0) | 2007.07.18 |
| splash_class_multi (0) | 2007.07.13 |
| splash_class (0) | 2007.07.13 |

