mathematical models
signals
scalar (monochrome image) / vector (color image) function
The domain of a given function is the set of "input" values for which the function is defined.
The range of a function is the set of all "output" values produced by that function.
12p
Image Functions
f(x,y) or f(x,y,t)
- perspective: parallel (or orthographic) projection
- static/dynamic, monochrome/color
- resolution: spatial/spectral/radiometric/time
- deterministic/stochastic
The 2D intensity image is the result of a perspective projection of the 3D scene.
13p
Parallel/Orthographic projection
http://en.wikipedia.org/wiki/Orthographic_projection
http://en.wikipedia.org/wiki/Orthographic_projection_(geometry)
http://en.wikipedia.org/wiki/Orthogonal_projection
http://en.wikipedia.org/wiki/Graphical_projection
A full 3D representation is
(1) independent of the viewpoint
(2) expressed in the co-ordinate system of the object (rather than of the viewer)
=> Any intensity image view of the objects may be synthesized by standard computer graphics techniques.
microstructure
http://en.wikipedia.org/wiki/Microstructure
14p
Quality of a digital image
1. spatial resolution
2. spectral resolution
3. radiometric resolution
4. time resolution
Images f(x,y)
: deterministic functions / realizations of stochastic processes
linear system theory
integral transforms
discrete mathematics
theory of stochastic processes
A 'well-behaved' image function f(x,y) is integrable, has an invertible Fourier transform, etc.
sampled - a matrix with M rows and N columns
quantization - K interval (an integer value)
Image quantization assigns to each continuous sample an integer value - the continuous range of the image function f(x,y) is split into K intervals.
2.2.1 Sampling
Shannon's theorem (->3.2.5)
http://en.wikipedia.org/wiki/Shannon%27s_theorem
In information theory, the noisy-channel coding theorem establishes that however contaminated with noise interference a communication channel may be, it is possible to communicate digital data (information) nearly error-free up to a given maximum rate through the channel. This surprising result, sometimes called the fundamental theorem of information theory, or just Shannon's theorem, was first presented by Claude Shannon in 1948.The Shannon limit or Shannon capacity of a communications channel is the theoretical maximum information transfer rate of the channel, for a particular noise level.
TV - 512 * 512
PAL - 768 * 576
NTSC - 640 * 480
15p
raster
: the grid on which a neighborhood relation between points is defined
http://en.wikipedia.org/wiki/Rasterisation
Dirac impulses
http://en.wikipedia.org/wiki/Dirac_delta_function
The pixel captured by a real digitization device has finite size, since the sampling function is not a collection of ideal Dirac impulses but a collection of limited impulses.
-> 3.2.5
2.2.2 Quantization
Quantization is the transition between continuous values of the image function (brightness) and its digital equivalent.
The number of brightness of displays normally provide a range of at least 100 intensity levels.
average local brightness => gray-scale transformation techniques
(-> 5.1.2)
2.3 Digital image properties
17p
2.3.1 Metric and topological properties of digital images
Distance - identity, symmetry, triangular inequality
1) Euclidean distance, D_E
Pythagorean metric
http://en.wikipedia.org/wiki/Euclidean_distance
2) 'city block' distance (; L1 metric; Manhattan distance), D_4
rectilinear distance, L1 distance or L1 norm (see Lp space), city block distance, Manhattan distance, or Manhattan length
http://en.wikipedia.org/wiki/City_block_distance
3) 'chessboard' distance, D_8
Chebyshev distance (or Tchebychev distance), or L∞ metric
http://en.wikipedia.org/wiki/Chebyshev_distance
4) quasi-Euclidean distance D_QE
18p
region
: a connected set (in a set theory)
: a set of pixels in which there is a path between any pair of its pixels, all of whose pixels also belong to the set
: a set of pixels in which each pair of pixels is contiguous
object (image data interpretation: segmentation)
hole
: points which do not belong to the object and are surrounded by the object
background
The relation 'to be contiguous' decomposes an image into individual regions.
19p
contiguity paradox
paradoxes of crossing lines
connectivity problems
ref.
Digital Geometry: Geometric Methods for Digital Picture Analysis
Reinhard Klette, Azriel Rosenfeld (Morgan Kaufmann, 2004)
topology based on cellular complexes
http://en.wikipedia.org/wiki/Bernhard_Riemann
http://en.wikipedia.org/wiki/Differential_geometry
ref.
Algorithms in Digital Geometry Based on Cellular Topology
University of Applied Sciences Berlin
http://www.kovalevsky.de/; kovalev@tfh-berlin.de
Abstract. The paper presents some algorithms in digital geometry based on the
topology of cell complexes. The paper contains an axiomatic justification of the
necessity of using cell complexes in digital geometry. Algorithms for solving
the following problems are presented: tracing of curves and surfaces,
recognition of digital straight line segments (DSS), segmentation of digital
curves into longest DSS, recognition of digital plane segments, computing the
curvature of digital curves, filling of interiors of n-dimensional regions
(n=2,3,4), labeling of components (n=2,3), computing of skeletons (n=2, 3).
20p
distance transform; distance function; chamfering algorithm
woodcarving operation
http://en.wikipedia.org/wiki/Distance_transform
ref.
Distance Transform
David Coeurjolly, Laboratoire LIRIS, France, 2006
A Method for Obtaining Skeletons Using a Quasi-Euclidean Distance
U Montanari - Journal of the ACM (JACM), 1968
A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions
Maurer, C.R., Jr.; Rensheng Qi; Raghavan, V
> applications of the distance transformation
discrete geometry
path planning and obstacle avoidance in mobile robotics
finding the closest feature in the image
skeletonization (mathematical morphology methods)
21p
edge
: a local property of a pixel and its immediate neighborhood
The edge tells us how fast the image intensity varies in a small neighborhood of a pixel.
crack edge
22p
border (boundary)
: the set of pixels within the region that have one or more neighbors outside
: inner/outer
The border is a global concept related to a region, while edge expresses local properties of an image function.
23p
convex
: If any two points within a region are connected by a straight line segment, and the whole line lies within the region, then this region is convex.
convex hull
: the smallest convex region containing the input region
deficit of convexity - lakes & bays
topology
topological invariant = topological invariant
http://en.wikipedia.org/wiki/Topological_property
a property of a topological space which is invariant under homeomorphisms. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.
homeomorphism = topological isomorphism
http://en.wikipedia.org/wiki/Homeomorphism
the mappings which preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.
rubber sheet transform:
Stretching does not change contiguity of the object parts and does not change the number of holes in regions.
Euler-Poincaré Characteristi
http://en.wikipedia.org/wiki/Euler_characteristic
http://mathworld.wolfram.com/EulerCharacteristic.html
24p
2.3.2 Histograms
brightness histogram
: the freqency of the brightness value in the image
The histogram is usually the only global information about the image which is available.
> applications of histogram
finding optimal illumination conditions for capturing an image
gray-scale transformations
image segmentation to objects and background
A change of the object position on a constant background does not affect the histogram.
> local smoothing of the histogram
(1) local averaging of neighboring histogram elements + boundary adjustment
(2) Gaussian blurring: 1-d simplification of the 2-d Gaussian blur
25p
2.3.3 Entropy
information entropy
: the amount of uncertainty about an event associated with a given probability distribution
As the level of disorder rises, entropy increases and events are less predictable.
The uncertainty for such set of  outcomes is defined by
outcomes is defined by
-
since the probability of each event is 1 / n, we can write
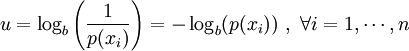
The average uncertainty  , with
, with  being the average operator, is obtained by
being the average operator, is obtained by
http://en.wikipedia.org/wiki/Entropy_(information_theory)
Shannon's source coding theorem shows that, in the limit, the average length of the shortest possible representation to encode the messages in a given alphabet is their entropy divided by the logarithm of the number of symbols in the target alphabet.
C.E. Shannon, "A Mathematical Theory of Communication",
Bell System Technical Journal, vol. 27, pp. 379-423, 623-656, July, October, 1948
2.3.4 Visual perception of the image- Contrast
- http://en.wikipedia.org/wiki/Contrast_(vision)
- Acuity 예민함
- http://en.wikipedia.org/wiki/Visual_acuity
- visual illusions
- http://en.wikipedia.org/wiki/Optical_illusion
- http://en.wikipedia.org/wiki/Ebbinghaus_illusion
- perceptual grouping -> image segmentation
- Gestalt theory
- http://en.wikipedia.org/wiki/Gestalt_psychology
-
Patterns take precedence over elements and have properties that are not inherent in the elements themselves.
- 28p
2.3.5 Image quality
- Azriel Rosenfeld, Avinash C. Kak, Digital Picture Processing, Academic Press, 1982
parameter optimization
correlation between images
resolution of small or proximate objects in the image
measures of image similarity (retrieval from image databases)
2.3.6 Noise in image
white noise
http://en.wikipedia.org/wiki/White_noise
-> Gaussian noise
additive noise
http://en.wikipedia.org/wiki/Additive_white_Gaussian_noise
multiplicative noise
quantization noise
http://en.wikipedia.org/wiki/Quantization_noise
impulse noise
-> salt-and-pepper noise
http://en.wikipedia.org/wiki/Salt_and_pepper_noise
unknown about noise properties -> local pre-processing methods
known noise parameters -> image restoration techniques
SNR = signal-to-noise ration
http://en.wikipedia.org/wiki/Signal-to-noise_ratio
2.4 Color images
2.4.1 Physics of color
2.4.2 Color perceived by humans
2.4.3 Color spaces
2.4.4 Palette images
2.4.5 Color constancy
2.5 Cameras: an overview
2.5.1 Photosensitive sensors
2.5.2 A monochromatic camera
2.5.3 A color camera
2.6 Summary
'@GSMC > 박래홍: Computer Vision' 카테고리의 다른 글
| Ch.10 Image Understanding (0) | 2008.12.15 |
|---|---|
| Ch.9 Object Recognition (0) | 2008.11.25 |
| 2.4 Color images & 2.5 Cameras (0) | 2008.10.16 |
| Ch. 6 Segmentation I (0) | 2008.09.20 |
| Ch.1 Introduction (0) | 2008.09.04 |

 kovalevski.pdf
kovalevski.pdf
